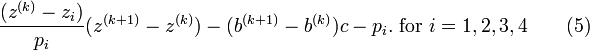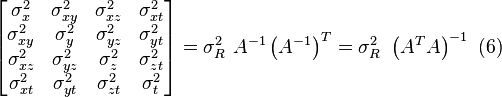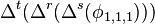Global Positioning System
| It has been suggested that Introduction to the Global Positioning System be merged into this article or section. (Discuss) |

Civilian GPS receiver ("GPS navigation device") in a marine application. 
Automotive navigation system in a taxicab. |
The Global Positioning System (GPS) is a space-based global navigation satellite system that provides reliable location and time information in all weather and at all times and anywhere on or near the Earth when and where there is an unobstructed line of sight to four or more GPS satellites. It is maintained by the United States government and is freely accessible by anyone with a GPS receiver.
GPS was created and realized by the U.S. Department of Defense (DOD) and was originally run with 24 satellites. It was established in 1973 to overcome the limitations of previous navigation systems.[1]
[edit] Structure

GPS consists of three parts: the space segment, the control segment, and the user segment. The U.S. Air Force develops, maintains, and operates the space and control segments. GPS satellites broadcast signals from space, which each GPS receiver uses to calculate its three-dimensional location (latitude, longitude, and altitude) plus the current time.[2]
The space segment is composed of 24 to 32 satellites in medium Earth orbit and also includes the boosters required to launch them into orbit. The control segment is composed of a master control station, an alternate master control station, and a host of dedicated and shared ground antennas and monitor stations. The user segment is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial, and scientific users of the Standard Positioning Service (see GPS navigation devices).
[edit] Applications
While originally a military project, GPS is considered a dual-use technology, meaning it has significant military and civilian applications.
GPS has become a widely used and a useful tool for commerce, scientific uses, tracking and surveillance. GPS's accurate timing facilitates everyday activities such as banking, mobile phone operations, and even the control of power grids. Farmers, surveyors, geologists and countless others perform their work more efficiently, safely, economically, and accurately.[2]
[edit] Civilian

Many civilian applications use one or more of GPS's three basic components: absolute location, relative movement, and time transfer.
- Surveying: Surveyors use absolute locations to make maps and determine property boundaries
- Map-making: Both civilian and military cartographers use GPS extensively.
- Navigation: Navigators value digitally precise velocity and orientation measurements.
- Cellular telephony: Clock synchronization enables time transfer, which is critical for synchronizing its spreading codes with other base stations to facilitate inter-cell handoff and support hybrid GPS/cellular position detection for mobile emergency calls and other applications. The first handsets with integrated GPS launched in the late 1990s. The U.S. Federal Communications Commission (FCC) mandated the feature in 2002 so emergency services could locate 911 callers. Third-party software developers later gained access to GPS APIs from Nextel upon launch, followed by Sprint in 2006, and Verizon soon thereafter.
- Tectonics: GPS enables direct fault motion measurement in earthquakes.
- Disaster relief/emergency services: Depend upon GPS for location and timing capabilities
- GPS tours: Location determines which content to display; for instance, information about an approaching point of interest is displayed.
- Geofencing: Vehicle tracking systems, person tracking systems, and pet tracking systems use GPS to locate a vehicle, person, or pet. These devices attach to the vehicle, person, or the pet collar. The application provides 24/7 tracking and mobile or Internet updates should the trackee leave a designated area.[3]
- Recreation: For example, geocaching, geodashing, GPS drawing and waymarking
- GPS Aircraft Tracking
- Geotagging: Applying location coordinates to digital objects such as photographs and other documents for purposes such as creating map overlays. only a few Digital camera is GPS enabled. one of them is variant of the Single-lens translucent camera Sony SLT-A55V and will be sold in most markets (not all markets).[4]
[edit] Restrictions on civilian use
The U.S. Government controls the export of some civilian receivers. All GPS receivers capable of functioning above 18 kilometers (11 mi) altitude and 515 metres per second (1,001 kn)[5] are classified as munitions (weapons) for which U.S. State Department export licenses are required. These limits attempt to prevent use of a receiver in a ballistic missile. They would not prevent use in a cruise missile since their altitudes and speeds are similar to those of ordinary aircraft.
This rule applies even to otherwise purely civilian units that only receive the L1 frequency and the C/A code and cannot correct for SA, etc.
Disabling operation above these limits exempts the receiver from classification as a munition. Vendor interpretations differ. The rule targets operation given the combination of altitude and speed, while some receivers stop operating even when stationary. This has caused problems with some amateur radio balloon launches, which regularly reach 30 kilometers (19 mi).
[edit] Military
As of 2009, military applications of GPS include:
- Navigation: GPS allows soldiers to find objectives, even in the dark or in unfamiliar territory, and to coordinate troop and supply movement. In the US armed forces, commanders use the Commanders Digital Assistant and lower ranks use the Soldier Digital Assistant.[6][7][8][9]
- Target tracking: Various military weapons systems use GPS to track potential ground and air targets before flagging them as hostile.[citation needed] These weapon systems pass target coordinates to precision-guided munitions to allow them to engage targets accurately. Military aircraft, particularly in air-to-ground roles, use GPS to find targets (for example, gun camera video from AH-1 Cobras in Iraq show GPS co-ordinates that can be looked up in Google Earth).
- Missile and projectile guidance: GPS allows accurate targeting of various military weapons including ICBMs, cruise missiles and precision-guided munitions. Artillery projectiles. Embedded GPS receivers able to withstand accelerations of 12,000 g or about 118 km/s2 have been developed for use in 155 millimeters (6.1 in) howitzers.[10]
- Search and Rescue: Downed pilots can be located faster if their position is known.
- Reconnaissance: Patrol movement can be managed more closely.
- GPS satellites carry a set of nuclear detonation detectors consisting of an optical sensor (Y-sensor), an X-ray sensor, a dosimeter, and an electromagnetic pulse (EMP) sensor (W-sensor), which form a major portion of the United States Nuclear Detonation Detection System.[11][12]
[edit] History
The design of GPS is based partly on similar ground-based radio navigation systems, such as LORAN and the Decca Navigator developed in the early 1940s, and used during World War II. In 1956 Friedwardt Winterberg[13] proposed a test of general relativity using accurate atomic clocks placed in orbit in artificial satellites. To achieve accuracy requirements, GPS uses principles of general relativity to correct the satellites' atomic clocks. Additional inspiration for GPS came when the Soviet Union launched the first man-made satellite, Sputnik in 1957. A team of U.S. scientists led by Dr. Richard B. Kershner were monitoring Sputnik's radio transmissions. They discovered that, because of the Doppler effect, the frequency of the signal being transmitted by Sputnik was higher as the satellite approached, and lower as it continued away from them. They realized that since they knew their exact location on the globe, they could pinpoint where the satellite was along its orbit by measuring the Doppler distortion (see Transit (satellite)).
The first satellite navigation system, Transit, used by the United States Navy, was first successfully tested in 1960. It used a constellation of five satellites and could provide a navigational fix approximately once per hour. In 1967, the U.S. Navy developed the Timation satellite that proved the ability to place accurate clocks in space, a technology that GPS relies upon. In the 1970s, the ground-based Omega Navigation System, based on phase comparison of signal transmission from pairs of stations,[14] became the first worldwide radio navigation system. However, limitations of these systems drove the need for a more universal navigation solution with greater accuracy.
While there were wide needs for accurate navigation in military and civilian sectors, almost none of those were seen as justification for the billions of dollars it would cost in research, development, deployment, and operation for a complex constellation of navigation satellites. However during the Cold War arms race, the nuclear threat to the very existence of the United States was the one need that did justify this cost in the view of the US Congress. This deterrent effect is why GPS was funded. The nuclear triad consisted of the US Navy's submarine-launched ballistic missiles (SLBMs) along with the US Air Force's strategic bombers and intercontinental ballistic missiles (ICBMs). Considered vital to the nuclear deterrence posture, accurate determination of the SLBM launch position was a force multiplier.
Precise navigation would enable US submarines to get an accurate fix of their positions prior to launching their SLBMs.[15] The US Air Force with two-thirds of the nuclear triad also had requirements for a more accurate and reliable navigation system. The Navy and Air Force were developing their own technologies in parallel to solve what was essentially the same problem. To increase the survivability of ICBMs, there was a proposal to use mobile launch platforms so the need to fix the launch position had similarity to the SLBM situation.
In 1960, the Air Force proposed a radio-navigation system called MOSAIC (Mobile System for Accurate ICBM Control) that was essentially a 3-D LORAN. A follow-on study called Project 57 was worked in 1963 and it was "in this study that the GPS concept was born." That same year the concept was pursued as Project 621B, which had "many of the attributes that you now see in GPS"[16] and promised increased accuracy for Air Force bombers as well as ICBMs. Updates from the Navy Transit system were too slow for the high speeds that the Air Force operated at. The Navy Research Laboratory continued advancements with their Timation (Time Navigation) satellites, first launched in 1967, and with the third one in 1974 carrying the first atomic clock put into orbit.[17]
With these parallel developments out of the 1960s, it was realized that a superior system could be developed by synthesizing the best technologies from 621B, Transit, Timation and SECOR in a multi-service program. Over the Labor Day weekend in 1973, a meeting of about 12 military officers at the Pentagon discussed the creation of a Defense Navigation Satellite System (DNSS). It was at this meeting that "the real synthesis that became GPS was created." Later that year, the DNSS program was named Navstar. With the individual satellites being associated with the name Navstar (as with the predecessors Transit and Timation), a more fully encompassing name was used to identify the constellation of Navstar satellites. This more complete name was Navstar-GPS, which was later shortened simply to GPS.[18]
After Korean Air Lines Flight 007, carrying 269 people, was shot down in 1983 after straying into the USSR's prohibited airspace,[19] in the vicinity of Sakhalin and Moneron Islands, President Ronald Reagan issued a directive making GPS freely available for civilian use, once it was sufficiently developed, as a common good.[20] The first satellite was launched in 1989, and the 24th satellite was launched in 1994.
Initially, the highest quality signal was reserved for military use, and the signal available for civilian use was intentionally degraded ("Selective Availability", SA). This changed with U.S. President Bill Clinton ordering Selective Availability turned off at midnight May 1, 2000, improving the precision of civilian GPS from 300 meters (about 1000 feet) to 20 meters (about 65 feet). The U.S. military by then had the ability to deny GPS service to potential adversaries on a regional basis.[21]
[edit] Timeline and modernization
| Block | Launch Period |
Satellite launches | Currently in orbit and healthy | |||
|---|---|---|---|---|---|---|
| Suc- cess |
Fail- ure |
In prep- aration |
Plan- ned | |||
| I | 1978–1985 | 10 | 1 | 0 | 0 | 0 |
| II | 1989–1990 | 9 | 0 | 0 | 0 | 0 |
| IIA | 1990–1997 | 19 | 0 | 0 | 0 | 10 of the 19 launched |
| IIR | 1997–2004 | 12 | 1 | 0 | 0 | 12 of the 13 launched |
| IIR-M | 2005–2009 | 8 | 0 | 0 | 0 | 7 of the 8 launched |
| IIF | 2010–2011 | 1 | 0 | 11 | 0 | 1 of the 1 launched |
| IIIA | 2014–? | 0 | 0 | 0 | 12 | 0 |
| IIIB | 0 | 0 | 0 | 8 | 0 | |
| IIIC | 0 | 0 | 0 | 16 | 0 | |
| Total | 59 | 2 | 11 | 36 | 30 | |
| (Last update: 24 May 2010) PRN 01 from Block IIR-M is unhealthy | ||||||
- In 1972, the U.S. Air Force Central Inertial Guidance Test Facility (Holloman AFB), conducted developmental flight tests of two prototype GPS receivers over White Sands Missile Range, using ground-based pseudo-satellites.
- In 1978, the first experimental Block-I GPS satellite was launched.
- In 1983, after Soviet interceptor aircraft shot down the civilian airliner KAL 007 that strayed into prohibited airspace due to navigational errors, killing all 269 people on board, U.S. President Ronald Reagan announced that GPS would be made available for civilian uses once it was completed.[24][25]
- By 1985, ten more experimental Block-I satellites had been launched to validate the concept.
- On February 14, 1989, the first modern Block-II satellite was launched.
- The Gulf War from 1990 to 1992, was the first conflict where GPS was widely used.[26]
- In 1992, the 2nd Space Wing, which originally managed the system, was de-activated and replaced by the 50th Space Wing.
- By December 1993, GPS achieved initial operational capability.[citation needed]
- By January 17, 1994 a complete constellation of 24 satellites was in orbit.
- Full Operational Capability was declared by NAVSTAR in April 1995.
- In 1996, recognizing the importance of GPS to civilian users as well as military users, U.S. President Bill Clinton issued a policy directive[27] declaring GPS to be a dual-use system and establishing an Interagency GPS Executive Board to manage it as a national asset.
- In 1998, U.S. Vice President Al Gore announced plans to upgrade GPS with two new civilian signals for enhanced user accuracy and reliability, particularly with respect to aviation safety and in 2000 the U.S. Congress authorized the effort, referring to it as GPS III.
- In 1998, GPS technology was inducted into the Space Foundation Space Technology Hall of Fame.
- On May 2, 2000 "Selective Availability" was discontinued as a result of the 1996 executive order, allowing users to receive a non-degraded signal globally.
- In 2004, the United States Government signed an agreement with the European Community establishing cooperation related to GPS and Europe's planned Galileo system.
- In 2004, U.S. President George W. Bush updated the national policy and replaced the executive board with the National Executive Committee for Space-Based Positioning, Navigation, and Timing.[28]
- November 2004, QUALCOMM announced successful tests of assisted GPS for mobile phones.[29]
- In 2005, the first modernized GPS satellite was launched and began transmitting a second civilian signal (L2C) for enhanced user performance.
- On September 14, 2007, the aging mainframe-based Ground Segment Control System was transferred to the new Architecture Evolution Plan.[30]
- The most recent launch was on May 28, 2010.[31] The oldest GPS satellite still in operation was launched on November 26, 1990, and became operational on December 10, 1990.[32]
- On May 19, 2009, the U. S. Government Accountability Office issued a report warning that some GPS satellites could fail as soon as 2010.[33]
- On May 21, 2009, the Air Force Space Command allayed fears of GPS failure saying "There's only a small risk we will not continue to exceed our performance standard."[34]
- On January 11, 2010, an update of ground control systems caused a software incompatibility with 8000 to 10000 military receivers manufactured by a division of Trimble Navigation Limited of Sunnyvale, Calif.[35]
[edit] Awards
Two GPS developers received the National Academy of Engineering Charles Stark Draper Prize for 2003:
- Ivan Getting, emeritus president of The Aerospace Corporation and engineer at the Massachusetts Institute of Technology, established the basis for GPS, improving on the World War II land-based radio system called LORAN (Long-range Radio Aid to Navigation).
- Bradford Parkinson, professor of aeronautics and astronautics at Stanford University, conceived the present satellite-based system in the early 1960s and developed it in conjunction with the U.S. Air Force. Parkinson served twenty-one years in the Air Force, from 1957 to 1978, and retired with the rank of colonel.
GPS developer Roger L. Easton received the National Medal of Technology on February 13, 2006.[36]
On February 10, 1993, the National Aeronautic Association selected the GPS Team as winners of the 1992 Robert J. Collier Trophy, the nation's most prestigious aviation award. This team combines researchers from the Naval Research Laboratory, the U.S. Air Force, the Aerospace Corporation, Rockwell International Corporation, and IBM Federal Systems Company. The citation honors them "for the most significant development for safe and efficient navigation and surveillance of air and spacecraft since the introduction of radio navigation 50 years ago."
[edit] Basic concept of GPS
A GPS receiver calculates its position by precisely timing the signals sent by GPS satellites high above the Earth. Each satellite continually transmits messages that include
- the time the message was transmitted
- precise orbital information (the ephemeris)
- the general system health and rough orbits of all GPS satellites (the almanac).
The receiver utilizes the messages it receives to determine the transit time of each message and computes the distances to each satellite. These distances along with the satellites' locations are used with the possible aid of trilateration, depending on which algorithm is used, to compute the position of the receiver. This position is then displayed, perhaps with a moving map display or latitude and longitude; elevation information may be included. Many GPS units show derived information such as direction and speed, calculated from position changes.
Three satellites might seem enough to solve for position, since space has three dimensions and a position near the Earth's surface can be assumed. However, even a very small clock error multiplied by the very large speed of light[37] — the speed at which satellite signals propagate — results in a large positional error. Therefore receivers use four or more satellites to solve for the receiver's location and time. The very accurately computed time is effectively hidden by most GPS applications, which use only the location. A few specialized GPS applications do however use the time; these include time transfer, traffic signal timing, and synchronization of cell phone base stations.
Although four satellites are required for normal operation, fewer apply in special cases. If one variable is already known, a receiver can determine its position using only three satellites. (For example, a ship or plane may have known elevation.) Some GPS receivers may use additional clues or assumptions (such as reusing the last known altitude, dead reckoning, inertial navigation, or including information from the vehicle computer) to give a less accurate (degraded) position when fewer than four satellites are visible.[38][39][40]
[edit] Position calculation introduction
To provide an introductory description of how a GPS receiver works, errors will be ignored in this section. Using messages received from a minimum of four visible satellites, a GPS receiver is able to determine the times sent and then the satellite positions corresponding to these times sent. The x, y, and z components of position, and the time sent, are designated as ![\scriptstyle\left[x_i,\, y_i,\, z_i,\, t_i\right]](http://upload.wikimedia.org/math/1/e/3/1e337e4d6474fe7a49792005b63358d1.png) where the subscript i is the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received
where the subscript i is the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received  , the GPS receiver can compute the transit time of the message as
, the GPS receiver can compute the transit time of the message as  . Assuming the message traveled at the speed of light, c, the distance traveled or pseudorange,
. Assuming the message traveled at the speed of light, c, the distance traveled or pseudorange,  can be computed as
can be computed as  .
.
A satellite's position and pseudorange define a sphere, centered on the satellite with radius equal to the pseudorange. The position of the receiver is somewhere on the surface of this sphere. Thus with four satellites, the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver would be at a precise intersection of the four surfaces.
If the surfaces of two spheres intersect at more than one point, they intersect in a circle. The article trilateration shows this mathematically. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below.
The intersection of a third spherical surface with the first two will be its intersection with that circle; in most cases of practical interest, this means they intersect at two points.[41] Another figure, Surface of Sphere Intersecting a Circle (not a solid disk) at Two Points, illustrates the intersection. The two intersections are marked with dots. Again the article trilateration clearly shows this mathematically.
For automobiles and other near-earth-vehicles, the correct position of the GPS receiver is the intersection closest to the Earth's surface.[42] For space vehicles, the intersection farthest from Earth may be the correct one.
The correct position for the GPS receiver is also the intersection closest to the surface of the sphere corresponding to the fourth satellite.
[edit] Correcting a GPS receiver's clock
The method of calculating position for the case of no errors has been explained. one of the most significant error sources is the GPS receiver's clock. Because of the very large value of the speed of light, c, the estimated distances from the GPS receiver to the satellites, the pseudoranges, are very sensitive to errors in the GPS receiver clock. This suggests that an extremely accurate and expensive clock is required for the GPS receiver to work. on the other hand, manufacturers prefer to build inexpensive GPS receivers for mass markets. The solution for this dilemma is based on the way sphere surfaces intersect in the GPS problem.
It is likely that the surfaces of the three spheres intersect, since the circle of intersection of the first two spheres is normally quite large, and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three, since any clock error could cause it to miss intersecting a point. However, the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let  denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let
denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let 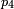 denote the pseudorange of the fourth satellite. Let
denote the pseudorange of the fourth satellite. Let 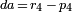 .
.  is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient,
is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient,  , provides an estimate of
, provides an estimate of
- (correct time) − (time indicated by the receiver's on-board clock),
and the GPS receiver clock can be advanced if  is positive or delayed if
is positive or delayed if  is negative. However, it should be kept in mind that a less simple function of
is negative. However, it should be kept in mind that a less simple function of  may be needed to estimate the time error in an iterative algorithm as discussed in the Navigation section.
may be needed to estimate the time error in an iterative algorithm as discussed in the Navigation section.
[edit] System segmentation

The current GPS consists of three major segments. These are the space segment (SS), a control segment (CS), and a user segment (US).[43]
[edit] Space segment
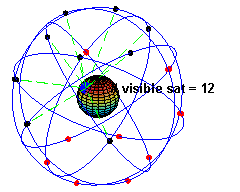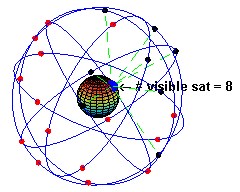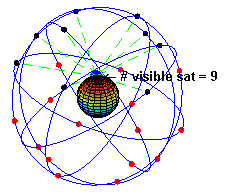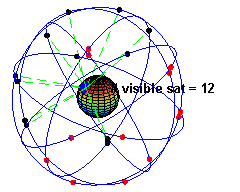
The space segment (SS) is composed of the orbiting GPS satellites, or Space Vehicles (SV) in GPS parlance. The GPS design originally called for 24 SVs, eight each in three circular orbital planes,[44] but this was modified to six planes with four satellites each.[45] The orbital planes are centered on the Earth, not rotating with respect to the distant stars.[46] The six planes have approximately 55° inclination (tilt relative to Earth's equator) and are separated by 60° right ascension of the ascending node (angle along the equator from a reference point to the orbit's intersection).[47] The orbits are arranged so that at least six satellites are always within line of sight from almost everywhere on Earth's surface.[48]
Orbiting at an altitude of approximately 20,200 kilometers (about 12,550 miles or 10,900 nautical miles; orbital radius of approximately 26,600 km (about 16,500 mi or 14,400 NM)), each SV makes two complete orbits each sidereal day, repeating the same ground track each day.[49] This was very helpful during development, since even with just four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones.
As of March 2008[update],[50] there are 31 actively broadcasting satellites in the GPS constellation, and two older, retired from active service satellites kept in the constellation as orbital spares. The additional satellites improve the precision of GPS receiver calculations by providing redundant measurements. With the increased number of satellites, the constellation was changed to a nonuniform arrangement. Such an arrangement was shown to improve reliability and availability of the system, relative to a uniform system, when multiple satellites fail.[51] About eight satellites are visible from any point on the ground at any one time (see animation at right).
[edit] Control segment
The control segment is composed of
- a master control station (MCS),
- an alternate master control station,
- four dedicated ground antennas and
- six dedicated monitor stations.
The MCS can also access U.S. Air Force Satellite Control Network (AFSCN) ground antennas (for additional command and control capability) and NGA (National Geospatial-Intelligence Agency) monitor stations. The flight paths of the satellites are tracked by dedicated U.S. Air Force monitoring stations in Hawaii, Kwajalein, Ascension Island, Diego Garcia, Colorado Springs, Colorado and Cape Canaveral, along with shared NGA monitor stations operated in England, Argentina, Ecuador, Bahrain, Australia and Washington DC.[52] The tracking information is sent to the Air Force Space Command's MCS at Schriever Air Force Base 25 km (16 miles) ESE of Colorado Springs, which is operated by the 2nd Space Operations Squadron (2 SOPS) of the United States Air Force (USAF). Then 2 SOPS contacts each GPS satellite regularly with a navigational update using dedicated or shared (AFSCN) ground antennas (GPS dedicated ground antennas are located at Kwajalein, Ascension Island, Diego Garcia, and Cape Canaveral). These updates synchronize the atomic clocks on board the satellites to within a few nanoseconds of each other, and adjust the ephemeris of each satellite's internal orbital model. The updates are created by a Kalman filter, which uses inputs from the ground monitoring stations, space weather information, and various other inputs.[53]
Satellite maneuvers are not precise by GPS standards. So to change the orbit of a satellite, the satellite must be marked unhealthy, so receivers will not use it in their calculation. Then the maneuver can be carried out, and the resulting orbit tracked from the ground. Then the new ephemeris is uploaded and the satellite marked healthy again.
[edit] User segment
The user segment is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial and scientific users of the Standard Positioning Service. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly stable clock (often a crystal oscillator). They may also include a display for providing location and speed information to the user. A receiver is often described by its number of channels: this signifies how many satellites it can monitor simultaneously. Originally limited to four or five, this has progressively increased over the years so that, as of 2007[update], receivers typically have between 12 and 20 channels.[54]

GPS receivers may include an input for differential corrections, using the RTCM SC-104 format. This is typically in the form of an RS-232 port at 4,800 bit/s speed. Data is actually sent at a much lower rate, which limits the accuracy of the signal sent using RTCM. Receivers with internal DGPS receivers can outperform those using external RTCM data. As of 2006[update], even low-cost units commonly include Wide Area Augmentation System (WAAS) receivers.
Many GPS receivers can relay position data to a PC or other device using the NMEA 0183 protocol, or the newer and less widely used NMEA 2000.[55] Although these protocols are officially defined by the National Marine Electronics Association (NMEA),[56] references to these protocols have been compiled from public records, allowing open source tools like gpsd to read the protocol without violating intellectual property laws. Other proprietary protocols exist as well, such as the SiRF and MTK protocols. Receivers can interface with other devices using methods including a serial connection, USB, or Bluetooth.
[edit] Communication
The navigational signals transmitted by GPS satellites encode a variety of information including satellite positions, the state of the internal clocks, and the health of the network. These signals are transmitted on two separate carrier frequencies that are common to all satellites in the network. Two different encodings are used, a public encoding that enables lower resolution navigation, and an encrypted encoding used by the U.S. military.
[edit] Message format
-
GPS message format Subframes Description 1 Satellite clock,
GPS time relationship2–3 Ephemeris
(precise satellite orbit)4–5 Almanac component
(satellite network synopsys,
error correction)
Each GPS satellite continuously broadcasts a navigation message at a rate of 50 bits per second (see bitrate). Each complete message is composed of 30-second frames, distinct groupings of 1,500 bits of information. Each frame is further subdivided into 5 subframes of length 6 seconds and with 300 bits each. Each subframe contains 10 words of 30 bits with length 0.6 seconds each. Each 30 second frame begins precisely on the minute or half minute as indicated by the atomic clock on each satellite.[57]
The first part of the message encodes the week number and the time within the week,[58] as well as the data about the health of the satellite. The second part of the message, the ephemeris, provides the precise orbit for the satellite. The last part of the message, the almanac, contains coarse orbit and status information for all satellites in the network as well as data related to error correction.[59]
All satellites broadcast at the same frequencies. Signals are encoded using code division multiple access (CDMA) allowing messages from individual satellites to be distinguished from each other based on unique encodings for each satellite (which the receiver must be aware of). Two distinct types of CDMA encodings are used: the coarse/acquisition (C/A) code, which is accessible by the general public, and the precise (P) code, that is encrypted so that only the U.S. military can access it.
The ephemeris is updated every 2 hours and is generally valid for 4 hours, with provisions for updates every 6 hours or longer in non-nominal conditions. The almanac is updated typically every 24 hours. Additionally data for a few weeks following is uploaded in case of transmission updates that delay data upload.
[edit] Satellite frequencies
All satellites broadcast at the same two frequencies, 1.57542 GHz (L1 signal) and 1.2276 GHz (L2 signal). The satellite network uses a CDMA spread-spectrum technique where the low-bitrate message data is encoded with a high-rate pseudo-random (PRN) sequence that is different for each satellite. The receiver must be aware of the PRN codes for each satellite to reconstruct the actual message data. The C/A code, for civilian use, transmits data at 1.023 million chips per second, whereas the P code, for U.S. military use, transmits at 10.23 million chips per second. The L1 carrier is modulated by both the C/A and P codes, while the L2 carrier is only modulated by the P code.[60] The P code can be encrypted as a so-called P(Y) code which is only available to military equipment with a proper decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.
[edit] Demodulation and decoding

Since all of the satellite signals are modulated onto the same L1 carrier frequency, there is a need to separate the signals after demodulation. This is done by assigning each satellite a unique binary sequence known as a Gold code. The signals are decoded, after demodulation, using addition of the Gold codes corresponding to the satellites monitored by the receiver.[61][62]
If the almanac information has previously been acquired, the receiver picks which satellites to listen for by their PRNs, unique numbers in the range 1 through 32. If the almanac information is not in memory, the receiver enters a search mode until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern. There can be a delay of up to 30 seconds before the first estimate of position because of the need to read the ephemeris data.
Processing of the navigation message enables the determination of the time of transmission and the satellite position at this time. For more information see Demodulation and Decoding, Advanced.
[edit]
The receiver uses messages received from four satellites to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as ![\ \left [x_i, y_i, z_i, t_i\right ]](http://upload.wikimedia.org/math/9/a/1/9a19680dd5a1e26d54fdf4c14685d54c.png) where the subscript i denotes the satellite and has the value 1, 2, 3, or 4. Knowing when the message was received
where the subscript i denotes the satellite and has the value 1, 2, 3, or 4. Knowing when the message was received  , the receiver computes the message's transit time as
, the receiver computes the message's transit time as  . Assuming the message traveled at the speed of light (c) the distance traveled,
. Assuming the message traveled at the speed of light (c) the distance traveled,  is
is  . Knowing the distance from receiver to satellite and the satellite's position implies that the receiver is on the surface of a sphere centered at the satellite's position. Thus the receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the receiver is at the intersection of the surfaces of four spheres. Excluding the unrealistic case (for GPS purposes) of two coincident spheres, the surfaces of two intersecting spheres is either a point (if they merely touch) or a circle as depicted in the illustration below. Two of the points at which the surfaces of the spheres intersect are clearly marked on the figure. The distance between these two points is the diameter of the circle of intersection.
. Knowing the distance from receiver to satellite and the satellite's position implies that the receiver is on the surface of a sphere centered at the satellite's position. Thus the receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the receiver is at the intersection of the surfaces of four spheres. Excluding the unrealistic case (for GPS purposes) of two coincident spheres, the surfaces of two intersecting spheres is either a point (if they merely touch) or a circle as depicted in the illustration below. Two of the points at which the surfaces of the spheres intersect are clearly marked on the figure. The distance between these two points is the diameter of the circle of intersection.
This can be seen more clearly by considering a side view of the intersecting spheres. This view would match the figure because of the symmetry of the spheres. A view from any horizontal direction would look exactly the same. Therefore the diameter as seen from all directions is the same and thus the surfaces actually do intersect in a circle. The article trilateration algebraically confirms this geometric argument that the two sphere surfaces intersect in a circle.
Having found that two sphere surfaces intersect in a circle, we now consider how the intersection of the first two sphere surfaces, the circle, intersect with the third sphere. A circle and sphere surface intersect at zero, one or two points. For the GPS problem we are concerned with the case of two points of intersection. Another figure, Surface of Sphere Intersecting a Circle (not a solid disk) at Two Points, is shown below to aid in visualizing this intersection. Trilateration algebraically confirms this geometric observation. The ambiguity of two points of intersection of three sphere surfaces can be resolved by noting which point is closest to the fourth sphere surface.
Having provided a discussion of how sphere surfaces intersect, we now formulate the equations for the case when errors are present.
Let  denote the clock error or bias, the amount by which the receiver's clock is off. The receiver has four unknowns, the three components of GPS receiver position and the clock bias
denote the clock error or bias, the amount by which the receiver's clock is off. The receiver has four unknowns, the three components of GPS receiver position and the clock bias ![\ \left [x, y, z, b\right ]](http://upload.wikimedia.org/math/e/5/7/e577dde7dce6b6ba43be7dd63e452f58.png) . The equation of the sphere surfaces are given by:
. The equation of the sphere surfaces are given by: ![(x-x_i)^2 + (y-y_i)^2 + (z-z_i)^2 = \bigl([tr_i + b - t_i]c\bigr)^2,](http://upload.wikimedia.org/math/8/2/d/82d0695c569f7f4d09ab06743c90ab77.png)
Another useful form of these equations is in terms of pseudoranges, which are the approximate ranges based on the receiver clock's uncorrected time so that  . Then the equations becomes:
. Then the equations becomes:
[edit]
- Bancroft's method is perhaps the most important method of solving the navigation equations since it involves an algebraic as opposed to numerical method.[63] The method requires at least four satellites but more can be used.
Two numerical methods of computing GPS receiver position and clock bias are (1) by using trilateration and one dimensional numerical root finding and (2) multidimensional Newton-Raphson calculations.
- The receiver can solve by trilateration[64][65] and one dimensional numerical root finding.[66] Trilateration determines the intersection of the surfaces of three spheres. In the usual case of two intersections, the point nearest the surface of the sphere corresponding to the fourth satellite is chosen. The Earth's surface can also sometimes be used instead, especially by civilian GPS receivers, since it is illegal in the United States to track vehicles more than 60,000 feet (18,000 m) in altitude. Let da denote the signed magnitude of the vector from the receiver position to the fourth satellite (i.e. da = r4 - p4) as defined in the section "Clock correction". da is a function of the correction since the correction changes the satellite transmission times and thus the pseudoranges. The notation, da(correction) denotes this function. The problem is to determine the correction such that
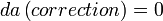 .
.
This is the familiar problem of finding the zeroes of a one dimensional non-linear function of a scalar variable. Iterative numerical methods, such as those found in the chapter on root finding in Numerical Recipes can solve this type of problem.[66] one advantage of this method is that it involves one dimensional as opposed to multidimensional numerical root finding.
- Alternatively, multidimensional root finding method such as Newton-Raphson method can be used.[66] The approach is to linearize around an approximate solution, say
![\ \left [x^{(k)}, y^{(k)}, z^{(k)}, b^{(k)}\right ]](http://upload.wikimedia.org/math/0/c/3/0c32ecd639a3623f156a678593d83504.png) from iteration k, then solve four linear equations derived from the quadratic equations above to obtain
from iteration k, then solve four linear equations derived from the quadratic equations above to obtain ![\left [x^{(k+1)}, y^{(k+1)}, z^{(k+1)}, b^{(k+1)}\right ]](http://upload.wikimedia.org/math/d/c/9/dc923433baae60fc389b303745ec2eb8.png) . The Newton-Raphson method is more rapidly convergent than other methods of numerical root finding.[66] A disadvantage of this multidimensional root finding method as compared to single dimensional root findiing is that, "There are no good general methods for solving systems of more than one nonlinear equations."[66] For a more detailed description of the mathematics see Multidimensional Newton Raphson.
. The Newton-Raphson method is more rapidly convergent than other methods of numerical root finding.[66] A disadvantage of this multidimensional root finding method as compared to single dimensional root findiing is that, "There are no good general methods for solving systems of more than one nonlinear equations."[66] For a more detailed description of the mathematics see Multidimensional Newton Raphson.
- When more than four satellites are available, the calculation can use the four best or more than four, considering number of channels, processing capability, and geometric dilution of precision (GDOP). Using more than four is an over-determined system of equations with no unique solution, which must be solved by least-squares or a similar technique.[63] If all visible satellites are used, the results are as good as or better than using the four best. Errors can be estimated through the residuals. With each combination of four or more satellites, a GDOP factor can be calculated, based on the relative sky directions of the satellites used.[67] As more satellites are picked up, pseudoranges from various 4-way combinations can be processed to add more estimates to the location and clock offset. The receiver then takes the weighted average of these positions and clock offsets. After the final location and time are calculated, the location is expressed in a specific coordinate system such as latitude and longitude, using the WGS 84 geodetic datum or a country-specific system.[68]
- Finally, results from other positioning systems such as GLONASS or the upcoming Galileo can be incorporated or used to check the result. (By design, these systems use the same frequency bands, so much of the receiver circuitry can be shared, though the decoding is different.)
[edit] Multidimensional Newton-Raphson for GPS
The equations used in multidimensional Newton-Raphson are as follows:
Let  and
and 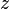 denote the true receiver position coordinates. Let
denote the true receiver position coordinates. Let  denote the unknown clock error or bias. Let the coordinates of each satellite, and the time the message was sent, be
denote the unknown clock error or bias. Let the coordinates of each satellite, and the time the message was sent, be ![\left [x_i, y_i, z_i, t_i\right ]](http://upload.wikimedia.org/math/3/6/7/3671904d39496edbe2ffcbaea29c28b1.png) , let the GPS clock's indicated received time be
, let the GPS clock's indicated received time be 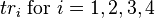 and c be the speed of light. The pseudorange is computed as:
and c be the speed of light. The pseudorange is computed as:
Assume the message travels at the speed of light, then the pseudorange satisfies the equation:
When an approximate solution, ![\left [x^{(k)}, y^{(k)}, z^{(k)}, b^{(k)}\right ]](http://upload.wikimedia.org/math/c/c/7/cc7b331eb4021f3a35c9e3b9f8418f59.png) rather than the exact solution,
rather than the exact solution, ![\left [x, y, z, b\right ]](http://upload.wikimedia.org/math/6/2/7/627e674407f7d7c9e6031ae343e8c934.png) is used in equation 1, there is a residual,
is used in equation 1, there is a residual, 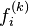 . Transforming
. Transforming 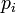 to the right hand side of the equation produces,
to the right hand side of the equation produces,
A solution will have been obtained when 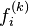 is zero or sufficiently close to zero for
is zero or sufficiently close to zero for  .
.
In order to linearize equation 2, the partial derivatives are computed as:
where
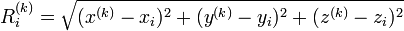 .
.
Linearizing the right hand side of equation 2 about the approximate solution, ![\left [x^{(k)}, y^{(k)}, z^{(k)}, b^{(k)}\right ]](http://upload.wikimedia.org/math/c/c/7/cc7b331eb4021f3a35c9e3b9f8418f59.png) there results
there results
where  is the residual due to linearization, which is in addition to the residual,
is the residual due to linearization, which is in addition to the residual,  , due to an approximate solution.
, due to an approximate solution.
In order to drive  closer to zero choose the values
closer to zero choose the values ![\left [x^{(k+1)}, y^{(k+1)}, z^{(k+1)}, b^{(k+1)}\right ]](http://upload.wikimedia.org/math/d/c/9/dc923433baae60fc389b303745ec2eb8.png) such that
such that
That is choose the values
such that the residual in equation 2 changes by approximately  as shown below.
as shown below.
Let
Substituting and transposing  to the left hand side of the equation, there results
to the left hand side of the equation, there results
Equations 6 provide four linear equations in four unknowns, the delta terms. They are in a form for solution. Using the values of  and
and 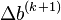 determined by this linear equation solution,
determined by this linear equation solution,
is evaluated using:
Then set  in equations 2 through 6, plug the terms
in equations 2 through 6, plug the terms
from equations 7 into equations 2, set  in equations 7, and reevaluate the residuals in equations 2. This procedure is repeated until the residuals are sufficiently small in magnitude.
in equations 7, and reevaluate the residuals in equations 2. This procedure is repeated until the residuals are sufficiently small in magnitude.
[edit] Error sources and analysis
| Source | Effect (m) |
|---|---|
| Signal arrival C/A | ±3 |
| Signal arrival P(Y) | ±0.3 |
| Ionospheric effects | ±5 |
| Ephemeris errors | ±2.5 |
| Satellite clock errors | ±2 |
| Multipath distortion | ±1 |
| Tropospheric effects | ±0.5 |
 C/A C/A |
±6.7 |
 P(Y) P(Y) |
±6.0 |
The term user equivalent range error (UERE) refers to the error of a component in the distance from receiver to a satellite. User equivalent range errors (UERE) are shown in the table. There is also a numerical error with an estimated value, 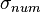 , of about 1 meter. The standard deviations,
, of about 1 meter. The standard deviations,  , for the coarse/acquisition and precise codes are also shown in the table. These standard deviations are computed by taking the square root of the sum of the squares of the individual components (i.e., RSS for root sum squares). To get the standard deviation of receiver position estimate, these range errors must be multiplied by the appropriate dilution of precision terms and then RSS'ed with the numerical error. Electronics errors are one of several accuracy-degrading effects outlined in the table above. When taken together, autonomous civilian GPS horizontal position fixes are typically accurate to about 15 meters (49 ft). These effects also reduce the more precise P(Y) code's accuracy. However, the advancement of technology means that today, civilian GPS fixes under a clear view of the sky are on average accurate to about 5 meters (16 ft) horizontally.
, for the coarse/acquisition and precise codes are also shown in the table. These standard deviations are computed by taking the square root of the sum of the squares of the individual components (i.e., RSS for root sum squares). To get the standard deviation of receiver position estimate, these range errors must be multiplied by the appropriate dilution of precision terms and then RSS'ed with the numerical error. Electronics errors are one of several accuracy-degrading effects outlined in the table above. When taken together, autonomous civilian GPS horizontal position fixes are typically accurate to about 15 meters (49 ft). These effects also reduce the more precise P(Y) code's accuracy. However, the advancement of technology means that today, civilian GPS fixes under a clear view of the sky are on average accurate to about 5 meters (16 ft) horizontally.
These UERE errors are given as ± errors thereby implying that they are unbiased or zero mean errors. These UERE errors are therefore used in computing standard deviations. The standard deviation of the error in receiver position,  , is computed by multiplying PDOP (Position Dilution Of Precision) by
, is computed by multiplying PDOP (Position Dilution Of Precision) by  , the standard deviation of the user equivalent range errors.
, the standard deviation of the user equivalent range errors.  is computed by taking the square root of the sum of the squares of the individual component standard deviations.
is computed by taking the square root of the sum of the squares of the individual component standard deviations.
PDOP is computed as a function of receiver and satellite positions. A detailed description of how to calculate PDOP is given in the section, geometric dilution of precision computation (GDOP).
 for the C/A code is given by:
for the C/A code is given by:
The standard deviation of the error in estimated receiver position  , again for the C/A code is given by:
, again for the C/A code is given by:
The error diagram on the left shows the inter relationship of indicated receiver position, true receiver position, and the intersection of the four sphere surfaces.
[edit] Signal arrival time measurement
The position calculation requires the current time, the position of the satellite and the measured delay of the received signal. Position accuracy is primarily dependent on the satellite position and signal delay.
To measure the delay, the receiver compares the bit sequence received from the satellite with an internally generated version. By comparing the rising and trailing edges of the bit transitions, modern electronics can measure signal offset to within about one percent of a bit pulse width,  , or approximately 10 nanoseconds for the C/A code. Since GPS signals propagate at the speed of light, this represents an error of about 3 meters.
, or approximately 10 nanoseconds for the C/A code. Since GPS signals propagate at the speed of light, this represents an error of about 3 meters.
This component of position accuracy can be improved by a factor of 10 using the higher-chiprate P(Y) signal. Assuming the same one percent of bit pulse width accuracy, the high-frequency P(Y) signal results in an accuracy of  or about 30 centimeters.
or about 30 centimeters.
[edit] Atmospheric effects
Atmospheric inconsistencies affect the speed of the GPS signals as they pass through the Earth's atmosphere, especially the ionosphere. Correcting these errors is a significant challenge to improving position accuracy. These effects are smallest for overhead satellites and greatest for satellites at the horizon since the path through the atmosphere is longer (see airmass). once the receiver's approximate location is known, a mathematical model can estimate and compensate for these errors.
Ionospheric microwave signal delay depends on its frequency. This phenomenon is known as dispersion and can be calculated from measurements of delays for two or more frequency bands, allowing delays at other frequencies to be estimated.[69] Some military and survey-grade civilian receivers calculate atmospheric dispersion from the different delays in the L1 and L2 frequencies, and apply a more precise correction. This can be done in civilian receivers without decrypting the P(Y) signal carried on L2, by tracking the carrier wave instead of the modulated code. To facilitate this on lower cost receivers, a new civilian code signal on L2, called L2C, was added to the Block IIR-M satellites, first launched in 2005. It allows a direct comparison of the L1 and L2 signals using the coded signal instead of the carrier wave.
Ionospheric effects generally change slowly, and can be averaged over time. Those for any particular geographical area can be easily calculated by comparing the measured position to a known surveyed location. This correction is also valid for other receivers in the same general location. Several systems send this information over radio or other links to allow L1-only receivers to make ionospheric corrections. The ionospheric data are transmitted via satellite in Satellite Based Augmentation Systems (SBAS) such as WAAS (available in North America and Hawaii), EGNOS (Europe and Asia) or MSAS (Japan), which transmits it on the GPS frequency using a special pseudo-random noise sequence (PRN), so only one receiver and antenna are required.
Humidity also causes a variable delay, resulting in errors similar to ionospheric delay, but occurring in the troposphere. This effect is both more localized and changes more quickly than ionospheric effects, and is not frequency dependent. These traits make precise measurement and compensation of humidity errors more difficult than ionospheric effects.[citation needed]
Changes in receiver altitude also change the delay, due to the signal passing through less of the atmosphere at higher elevations. Since the receiver computes its approximate altitude, this error is relatively simple to correct, either by applying a function regression or correlating margin of atmospheric error to ambient pressure using a barometric altimeter.[citation needed]
[edit] Multipath effects
GPS signals can be affected by multipath issues, where the radio signals reflect off surrounding terrain; buildings, canyon walls, hard ground, etc. These delayed signals can cause inaccuracy. A variety of techniques, most notably narrow correlator spacing, mitigate multipath errors. For long delay multipath, the receiver itself can recognize the wayward signal and discard it. To address shorter delay multipath from the signal reflecting off the ground, specialized antennae (e.g., a choke ring antenna) may be used to reduce the signal power as received by the antenna. Short delay reflections are harder to filter out because they interfere with the true signal, causing effects almost indistinguishable from routine fluctuations in atmospheric delay.
Multipath effects are much less severe in moving vehicles. When the antenna is moving, false solutions using reflected signals quickly fail to converge and only the direct signals result in stable solutions.
[edit] Ephemeris and clock errors
While ephemeris data is transmitted every 30 seconds, it may be up to two hours old. If a fast time to first fix (TTFF) is needed, it is possible to upload a valid ephemeris to a receiver, and in addition to setting the time, obtain a position fix in under ten seconds. It is feasible to put such ephemeris data on the web for use in mobile GPS devices.[70] See also Assisted GPS.
The satellite's atomic clocks experience noise and clock drift errors. The navigation message contains corrections for these errors and estimates of the accuracy of the atomic clock. However, they are based on observations and may not indicate the clock's current state.
These problems tend to be very small, but may add up to a few meters (tens of feet) of inaccuracy.[71]
For very precise positioning (e.g., in geodesy), these effects can be eliminated by differential GPS: the simultaneous use of two or more receivers at several survey points. In the 1990s when receivers were quite expensive, some methods of quasi-differential GPS were developed, using only one receiver with reoccupation of measuring points. At the TU Vienna the method was named qGPS and adequate post processing software was developed.
[edit] Geometric dilution of precision computation (GDOP)
When visible GPS satellites are adjacent in the sky (i.e., small angular separation), the DOP values are high; when far apart, the DOP values are low. Low DOP values represent a better GPS positional accuracy due to the wider angular separation. HDOP, VDOP, PDOP and TDOP are respectively Horizontal, Vertical, Position (3-D) and Time Dilution of Precision.
Figure 3.1 Dilution of Precision of[72] provides a graphical indication of how geometry affect accuracy.
We now take on the task of computing DOP terms. As a first step, consider the unit vector from the receiver to satellite i with components 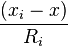 ,
,  , and
, and 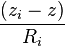 where the distance from receiver to the satellite,
where the distance from receiver to the satellite,  , is given by:
, is given by:
where x, y, and z denote the position of the receiver and  and zi denote the position of satellite i. These x, y, and z components may be components in a North, East, Down coordinate system a South, East, Up coordinate system or other convenient system. Formulate the matrix A as:
and zi denote the position of satellite i. These x, y, and z components may be components in a North, East, Down coordinate system a South, East, Up coordinate system or other convenient system. Formulate the matrix A as:
The first three elements of each row of A are the components of a unit vector from the receiver to the indicated satellite. The elements in the fourth column are c where c denotes the speed of light. Formulate the matrix, Q, as
The elements of the Q matrix are designated as:[73]
The Greek letter  is used quite often where we have used d. However the elements of the Q matrix do not represent variances and covariances as they are defined in probability and statistics. Instead they are strictly geometric terms. Therefore d as in dilution of precision is used. PDOP, TDOP and GDOP are given by
is used quite often where we have used d. However the elements of the Q matrix do not represent variances and covariances as they are defined in probability and statistics. Instead they are strictly geometric terms. Therefore d as in dilution of precision is used. PDOP, TDOP and GDOP are given by
 ,
,
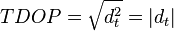 , and
, and

The horizontal dilution of precision, 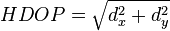 , and the vertical dilution of precision,
, and the vertical dilution of precision,  , are both dependent on the coordinate system used. To correspond to the local horizon plane and the local vertical, x, y, and z should denote positions in either a North, East, Down coordinate system or a South, East, Up coordinate system.
, are both dependent on the coordinate system used. To correspond to the local horizon plane and the local vertical, x, y, and z should denote positions in either a North, East, Down coordinate system or a South, East, Up coordinate system.
[edit] Derivation of DOP equations
Consider the position error vector,  , defined as the vector from the intersection of the four sphere surfaces corresponding to the pseudoranges to the true position of the receiver.
, defined as the vector from the intersection of the four sphere surfaces corresponding to the pseudoranges to the true position of the receiver. 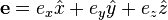 where bold denotes a vector and
where bold denotes a vector and 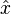 ,
, 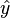 , and
, and 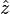 denote unit vectors along the x, y, and z axes respectively. Let
denote unit vectors along the x, y, and z axes respectively. Let 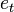 denote the time error, the true time minus the receiver indicated time. Assume that the mean value of the three components of
denote the time error, the true time minus the receiver indicated time. Assume that the mean value of the three components of  and
and 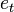 are zero.[75]
are zero.[75]
where  and
and  are the errors in pseudoranges 1 through 4 respectively. This equation comes from linearizing the equation relating pseudoranges to receiver position, satellite positions, and receiver clock errors as shown in.[76] Multiplying both sides by
are the errors in pseudoranges 1 through 4 respectively. This equation comes from linearizing the equation relating pseudoranges to receiver position, satellite positions, and receiver clock errors as shown in.[76] Multiplying both sides by  there results
there results
 .
.
Transposing both sides:
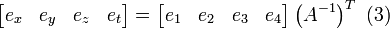 .
.
Post multiplying the matrices on both sides of equation (2) by the corresponding matrices in equation (3), there results
 .
.
Taking the expected value of both sides and taking the non-random matrices outside the expectation operator, E, there results:
Assuming the pseudorange errors are uncorrelated and have the same variance, the covariance matrix on the right side can be expressed as a scalar times the identity matrix. Thus
since 
Note:  since
since 
Substituting for  there follows
there follows
From equation (7), it follows that the variances of indicated receiver position and time are
 and
and

The remaining position and time error variance terms follow in a straightforward manner.
[edit] Selective availability
GPS includes a (currently disabled) feature called Selective Availability (SA) that adds intentional, time varying errors of up to 100 meters (328 ft) to the publicly available navigation signals. This was intended to deny an enemy the use of civilian GPS receivers for precision weapon guidance.
SA errors are actually pseudorandom, generated by a cryptographic algorithm from a classified seed key available only to authorized users (the U.S. military, its allies and a few other users, mostly government) with a special military GPS receiver. Mere possession of the receiver is insufficient; it still needs the tightly controlled daily key.
During the 1990-91 Gulf War, the shortage of military GPS units caused many U.S. troops and their families to buy readily–available civilian units. SA significantly impeded the U.S. military's battlefield use of GPS, so the military disabled SA for the duration of the war. Also during the 1990s, the FAA requested that the military turn off SA permanently to save millions of dollars annually to maintain their own radio navigation systems.[77]
Because SA affects every GPS receiver in a given area almost equally, a fixed station with an accurately known position can measure the SA error values and transmit them to the local GPS receivers so they may correct their position fixes. This is called Differential GPS or DGPS. DGPS also corrects for several other important sources of GPS errors, particularly ionospheric delay, so it continues to be widely used even though SA has been turned off. Typical SA errors were about 50 meters (164 ft) horizontally and about 100 m vertically. Widespread availability of DGPS nullified SA, leading to its demise on May 1, 2000.[78][clarification needed]
DGPS services are widely available from both commercial and government sources. The latter include WAAS and the U.S. Coast Guard's network of LF marine navigation beacons. The accuracy of the corrections depends on the distance between the user and the DGPS receiver. As distance increases, the errors at the two sites will not correlate as well, resulting in less precise differential corrections.
Per the directive, the induced error of SA was changed to add no error to the public signals (C/A code). Clinton's executive order required SA to be set to zero by 2006; it happened in 2000 once the U.S. military developed a new way to deny GPS (and other navigation services) to hostile forces in a specific area without affecting the rest of the world or its own military systems.[77]
One interesting side effect of the Selective Availability hardware is the capability to add corrections to the outgoing signal of the GPS cesium and rubidium atomic clocks to an accuracy of approximately 2 × 10−13. This represented a significant improvement over the clocks' raw accuracy.[citation needed]
On 19 September 2007, the United States Department of Defense announced that GPS III satellites need not implement SA,[79] eventually making the policy permanent.[80][81]
[edit] Antispoofing
Another restriction on GPS, antispoofing, remains on. This encrypts the P-code so that it cannot be mimicked by a transmitter sending false information. Few civilian receivers have ever used the P-code, and the accuracy attainable with the public C/A code is so much better than originally expected (especially with DGPS) that the antispoof policy has relatively little effect on most civilian users. Turning off antispoof would primarily benefit surveyors and some scientists who need extremely precise positions for experiments such as tracking tectonic plate motion.
[edit] Relativity
GPS positioning is one of the few everyday events in which relativistic effects must be accounted for.[82] For example, satellite clocks are tuned to 10.22999999543 MHz before launch, to compensate for the effects of gravitational time dilation and achieve a frequency of precisely 10.23 MHz once in orbit.[83] Some other relativistic effects (such as gravitational time delays, frequency shifts of clocks in satellites due to earth's quadrupole potential, and space curvature) are too small to affect the system at current accuracy levels.[84]
[edit] Special and general relativity
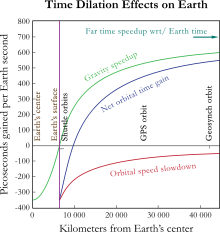
According to the theory of relativity, due to their constant movement and height relative to the Earth-centered, non-rotating approximately inertial reference frame, satellite clocks are affected by their speed. Special relativity predicts that the frequency of atomic clocks moving at orbital speeds tick more slowly than stationary ground clocks by a factor of  , a delay of about 7 μs/day, where the orbital velocity is v = 4 km/s, and c = the speed of light. The time dilation effect has been measured and verified using GPS.
, a delay of about 7 μs/day, where the orbital velocity is v = 4 km/s, and c = the speed of light. The time dilation effect has been measured and verified using GPS.
The gravitational frequency shift effect on GPS due to general relativity is that a clock closer to a massive object runs slower than a clock farther away. Applied to GPS, the receivers are much closer to Earth than the satellites, causing GPS clocks to be faster by a factor of 5×10−10, or about 45.9 μs/day.
When combining time dilation and gravitational frequency shift, the discrepancy is about 38 microseconds per day, a difference of 4.465 parts in 1010.[85] Without correction (i.e. without the solution algorithm correction for the initial pseudorange errors), errors in position determination of roughly 10 km/day would accumulate. In addition the elliptical, rather than perfectly circular, satellite orbits cause the time dilation and gravitational frequency shift effects to vary with time. This eccentricity effect causes the clock rate difference between a GPS satellite and a receiver to increase or decrease depending on the satellite's velocity orbital altitude.
To offset the discrepancy, the frequency standard on board each satellite is given a rate offset prior to launch, making it run slightly slower than the desired frequency on Earth; specifically, at 10.22999999543 MHz instead of 10.23 MHz.[86] Tuning the atomic clocks on GPS satellites makes the system a real-world engineering application of relativity.[87] Placing atomic clocks on artificial satellites to test Einstein's general theory was proposed by Friedwardt Winterberg in 1955.[88]
[edit] Sagnac distortion
GPS must also compensate for the Sagnac effect. The GPS time scale is defined in an inertial system but observations are processed in an Earth-centered, Earth-fixed (ECEF) co-rotating system, a system in which simultaneity is not uniquely defined. A Lorentz transformation converts from the inertial system to the ECEF system. The resulting correction has opposite algebraic signs for satellites in the Eastern and Western celestial hemispheres. Ignoring this effect produces an east-west error on the order of hundreds of nanoseconds, or tens of meters in position.[89]
[edit] Natural sources of interference
Since terrestrial GPS signals tend to be relatively weak, natural radio signals or scattering can desensitize the receiver, making acquiring and tracking satellite signals difficult or impossible.
Space weather degrades GPS operation in two ways, direct interference by solar radio burst noise in the same frequency band[90] or by scattering of the GPS radio signal in ionospheric irregularities referred to as scintillation.[91] Both forms of degradation follow the 11 year solar cycle and peak at sunspot maximum although they can occur anytime. Solar radio bursts are associated with solar flares and coronal mass ejections (CMEs)[92] and their impact can affect reception over the half of the Earth facing the sun. Scintillation occurs most frequently at tropical latitudes at night. It occurs less frequently at high latitudes or mid-latitudes where magnetic storms can lead to scintillation.[93] In addition to scintillation, magnetic storms can produce strong ionospheric gradients that degrade SBAS accuracy.[94]
[edit] Artificial sources of interference
In automotive GPS receivers, metallic features in windshields,[95] such as defrosters or car window tinting films,[96] can act as a Faraday cage, degrading reception inside the car.
Man-made electromagnetic interference (EMI) can also disrupt or jam GPS signals. In one well-documented case it was impossible to receive GPS signals in the entire harbor of Moss Landing, California due to unintentional jamming caused by malfunctioning TV antenna preamplifiers.[97][98] Intentional jamming is also possible. Generally, stronger signals can interfere with GPS receivers when they are within radio range or line of sight. In 2002 a detailed description of how to build a short-range GPS L1 C/A jammer was published in the online magazine Phrack.[99]
The U.S. government believes that such jammers were used occasionally during the 2001 war in Afghanistan, and the U.S. military claims to have destroyed six GPS jammers during the Iraq War, including one that was destroyed with a GPS-guided bomb.[100] A GPS jammer is relatively easy to detect and locate, making it an attractive target for anti-radiation missiles. The UK Ministry of Defence tested a jamming system in the UK's West Country on 7 and 8 June 2007.[101]
Some countries allow GPS repeaters, to facilitate the reception of GPS signals indoors and in obscured locations; however, under European Union and U.K. laws, these are prohibited because the signals can interfere with other GPS receivers that receive data from both satellites and the repeater.
Various techniques can address interference. one is to not rely on GPS as a sole source. According to John Ruley, "IFR pilots should have a fallback plan in case of a GPS malfunction".[102] Receiver Autonomous Integrity Monitoring (RAIM) is included in some receivers, to warn if jamming or another problem is detected. The U.S. military has also deployed since 2004 their Selective Availability / Anti-Spoofing Module (SAASM) in the Defense Advanced GPS Receiver (DAGR).[103] DAGR detects jamming and maintains its lock on encrypted GPS signals during interference.
[edit] Accuracy enhancement and surveying
[edit] Augmentation
Integrating external information into the calculation process can materially improve accuracy. Such augmentation systems are generally named or described based on how the information arrives. Some systems transmit additional error information (such as clock drift, ephemera, or ionospheric delay), others characterize prior errors, while a third group provides additional navigational or vehicle information.
Examples of augmentation systems include the Wide Area Augmentation System (WAAS), European Geostationary Navigation Overlay Service (EGNOS) , Differential GPS, Inertial Navigation Systems (INS) and Assisted GPS.
[edit] Precise monitoring
Accuracy can be improved through precise monitoring and measurement of existing GPS signals in additional or alternate ways.
The largest remaining error is usually the unpredictable delay through the ionosphere. The spacecraft broadcast ionospheric model parameters, but errors remain. This is one reason GPS spacecraft transmit on at least two frequencies, L1 and L2. Ionospheric delay is a well-defined function of frequency and the total electron content (TEC) along the path, so measuring the arrival time difference between the frequencies determines TEC and thus the precise ionospheric delay at each frequency.
Military receivers can decode the P(Y)-code transmitted on both L1 and L2. Without decryption keys, it is still possible to use a codeless technique to compare the P(Y) codes on L1 and L2 to gain much of the same error information. However, this technique is slow, so it is currently available only on specialized surveying equipment. In the future, additional civilian codes are expected to be transmitted on the L2 and L5 frequencies (see GPS modernization). Then all users will be able to perform dual-frequency measurements and directly compute ionospheric delay errors.
A second form of precise monitoring is called Carrier-Phase Enhancement (CPGPS). This corrects the error that arises because the pulse transition of the PRN is not instantaneous, and thus the correlation (satellite-receiver sequence matching) operation is imperfect. CPGPS utilizes the L1 carrier wave, which has a period of  which is about one-thousandth of the C/A Gold code bit period of
which is about one-thousandth of the C/A Gold code bit period of 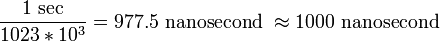 , to act as an additional clock signal and resolve the uncertainty. The phase difference error in the normal GPS amounts to 2–3 metres (6.6–9.8 ft) of ambiguity. CPGPS working to within 1% of perfect transition reduces this error to 3 centimeters (1.2 in) of ambiguity. By eliminating this error source, CPGPS coupled with DGPS normally realizes between 20–30 centimetres (7.9–12 in) of absolute accuracy.
, to act as an additional clock signal and resolve the uncertainty. The phase difference error in the normal GPS amounts to 2–3 metres (6.6–9.8 ft) of ambiguity. CPGPS working to within 1% of perfect transition reduces this error to 3 centimeters (1.2 in) of ambiguity. By eliminating this error source, CPGPS coupled with DGPS normally realizes between 20–30 centimetres (7.9–12 in) of absolute accuracy.
Relative Kinematic Positioning (RKP) is a third alternative for a precise GPS-based positioning system. In this approach, determination of range signal can be resolved to a precision of less than 10 centimeters (3.9 in). This is done by resolving the number of cycles in which the signal is transmitted and received by the receiver. This can be accomplished by using a combination of differential GPS (DGPS) correction data, transmitting GPS signal phase information and ambiguity resolution techniques via statistical tests—possibly with processing in real-time (real-time kinematic positioning, RTK).
[edit] Timekeeping
While most clocks are synchronized to Coordinated Universal Time (UTC), the atomic clocks on the satellites are set to GPS time. The difference is that GPS time is not corrected to match the rotation of the Earth, so it does not contain leap seconds or other corrections that are periodically added to UTC. GPS time was set to match Coordinated Universal Time (UTC) in 1980, but has since diverged. The lack of corrections means that GPS time remains at a constant offset with International Atomic Time (TAI) (TAI - GPS = 19 seconds). Periodic corrections are performed on the on-board clocks to correct relativistic effects and keep them synchronized with ground clocks.
The GPS navigation message includes the difference between GPS time and UTC, which as of 2009 is 15 seconds due to the leap second added to UTC December 31, 2008. Receivers subtract this offset from GPS time to calculate UTC and specific timezone values. New GPS units may not show the correct UTC time until after receiving the UTC offset message. The GPS-UTC offset field can accommodate 255 leap seconds (eight bits) which, given the current rate of change of the Earth's rotation (with one leap second introduced approximately every 18 months), should be sufficient to last until approximately the year 2300.
As opposed to the year, month, and day format of the Gregorian calendar, the GPS date is expressed as a week number and a seconds-into-week number. The week number is transmitted as a ten-bit field in the C/A and P(Y) navigation messages, and so it becomes zero again every 1,024 weeks (19.6 years). GPS week zero started at 00:00:00 UTC (00:00:19 TAI) on January 6, 1980, and the week number became zero again for the first time at 23:59:47 UTC on August 21, 1999 (00:00:19 TAI on August 22, 1999). To determine the current Gregorian date, a GPS receiver must be provided with the approximate date (to within 3,584 days) to correctly translate the GPS date signal. To address this concern the modernized GPS navigation message uses a 13-bit field, which only repeats every 8,192 weeks (157 years), thus lasting until the year 2137 (157 years after GPS week zero).
[edit] Carrier phase tracking (surveying)
Another method that is used in surveying applications is carrier phase tracking. The period of the carrier frequency times the speed of light gives the wavelength, which is about 0.19 meters for the L1 carrier. Accuracy within 1% of wavelength in detecting the leading edge, reduces this component of pseudorange error to as little as 2 millimeters. This compares to 3 meters for the C/A code and 0.3 meters for the P code.
However, 2 millimeter accuracy requires measuring the total phase—the number of waves times the wavelength plus the fractional wavelength, which requires specially equipped receivers. This method has many surveying applications.
Triple differencing followed by numerical root finding, and a mathematical technique called least squares can estimate the position of one receiver given the position of another. First, compute the difference between satellites, then between receivers, and finally between epochs. Other orders of taking differences are equally valid. Detailed discussion of the errors is omitted.
The satellite carrier total phase can be measured with ambiguity as to the number of cycles. Let  denote the phase of the carrier of satellite j measured by receiver i at time
denote the phase of the carrier of satellite j measured by receiver i at time  . This notation shows the meaning of the subscripts i, j, and k. The receiver (r), satellite (s), and time (t) come in alphabetical order as arguments of
. This notation shows the meaning of the subscripts i, j, and k. The receiver (r), satellite (s), and time (t) come in alphabetical order as arguments of  and to balance readability and conciseness, let
and to balance readability and conciseness, let  be a concise abbreviation. Also we define three functions, :
be a concise abbreviation. Also we define three functions, : , which return differences between receivers, satellites, and time points, respectively. Each function has variables with three subscripts as its arguments. These three functions are defined below. If
, which return differences between receivers, satellites, and time points, respectively. Each function has variables with three subscripts as its arguments. These three functions are defined below. If  is a function of the three integer arguments, i, j, and k then it is a valid argument for the functions, :
is a function of the three integer arguments, i, j, and k then it is a valid argument for the functions, :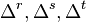 , with the values defined as
, with the values defined as
 ,
,
 , and
, and
 .
.
Also if 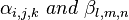 are valid arguments for the three functions and a and b are constants then
are valid arguments for the three functions and a and b are constants then 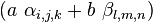 is a valid argument with values defined as
is a valid argument with values defined as
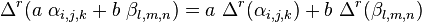 ,
,
 , and
, and
 .
.
Receiver clock errors can be approximately eliminated by differencing the phases measured from satellite 1 with that from satellite 2 at the same epoch.[104] This difference is designated as 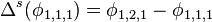
Double differencing[105] computes the difference of receiver 1's satellite difference from that of receiver 2. This approximately eliminates satellite clock errors. This double difference is:
Triple differencing[106] subtracts the receiver difference from time 1 from that of time 2. This eliminates the ambiguity associated with the integral number of wave lengths in carrier phase provided this ambiguity does not change with time. Thus the triple difference result eliminates practically all clock bias errors and the integer ambiguity. Atmospheric delay and satellite ephemeris errors have been significantly reduced. This triple difference is:
Triple difference results can be used to estimate unknown variables. For example if the position of receiver 1 is known but the position of receiver 2 unknown, it may be possible to estimate the position of receiver 2 using numerical root finding and least squares. Triple difference results for three independent time pairs quite possibly will be sufficient to solve for receiver 2's three position components. This may require the use of a numerical procedure.[107][108] An approximation of receiver 2's position is required to use such a numerical method. This initial value can probably be provided from the navigation message and the intersection of sphere surfaces. Such a reasonable estimate can be key to successful multidimensional root finding. Iterating from three time pairs and a fairly good initial value produces one observed triple difference result for receiver 2's position. Processing additional time pairs can improve accuracy, overdetermining the answer with multiple solutions. Least squares can estimate an overdetermined system. Least squares determines the position of receiver 2 which best fits the observed triple difference results for receiver 2 positions under the criterion of minimizing the sum of the squares.
[edit] Other systems
Other satellite navigation systems in use or various states of development include:
 Galileo – a global system being developed by the European Union and other partner countries, planned to be operational by 2014
Galileo – a global system being developed by the European Union and other partner countries, planned to be operational by 2014
 Beidou – People's Republic of China's regional system, covering Asia and the West Pacific[109]
Beidou – People's Republic of China's regional system, covering Asia and the West Pacific[109]
 COMPASS – People's Republic of China's global system, planned to be operational by 2020[110][111]
COMPASS – People's Republic of China's global system, planned to be operational by 2020[110][111]
 GLONASS – Russia's global navigation system
GLONASS – Russia's global navigation system
 IRNSS – India's regional navigation system, planned to be operational by 2012, covering India and Northern Indian Ocean[112]
IRNSS – India's regional navigation system, planned to be operational by 2012, covering India and Northern Indian Ocean[112]
 QZSS – Japanese proposed regional system covering only Japan
QZSS – Japanese proposed regional system covering only Japan
'연구하는 인생 > Technics' 카테고리의 다른 글
| HOW TO READ TIRE WEAR (0) | 2014.03.15 |
|---|---|
| Automatic transmission (0) | 2014.03.15 |
| GPS (0) | 2010.09.24 |
| 전류측정방법 (0) | 2009.06.26 |
| Clutch Hydraulic System (0) | 2008.03.26 |